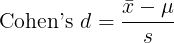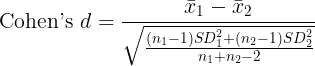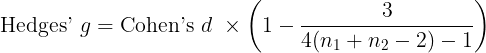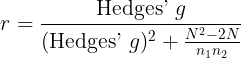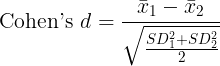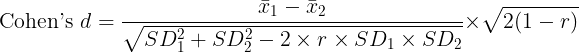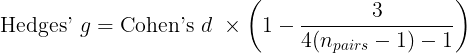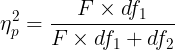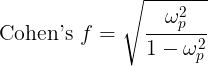Effect Size Calculators
Refer to this page for formulae and citations.
| Two groups | ANOVA, OLS & HLM |
|---|---|
| One-sample | Partial eta-squared (Fixed effects) |
| Independent-samples | R-squared (OLS) |
| Paired-samples | Intraclass Correlation Coefficient |
| Odds/risk/absolute ratios & NNT | HLM / multilevel Pseudo R-squared's |
Developed by James Uanhoro, when I was a graduate student within the Quantitative Research, Evaluation & Measurement program @ OSU.
I have run out of resources to sustain fitting the multilevel models, so for now, the ICC and multilevel R-squared sections are down.
All other components of this page have very low computational cost, so they will continue to function for the forseeable future.
One-sample t-test
Inputs
| Sample mean: | Population mean: |
| Sample standard deviation: | Sample size: |
| Confidence Interval: % | |
Results (CI using noncentral t distribution)
| Cohen's d: | |
| Lower limit on d: | Upper limit on d: |
Independent-samples t-test
Inputs
| Sample 1 | Sample 2 |
|---|---|
| Mean: | Mean: |
| Standard deviation: | Standard deviation: |
| Sample size: | Sample size: |
| Confidence Interval: % | |
Results (CI using noncentral t distribution)
| Hedges' g (Unbiased): | Lower limit on d: |
| Conversion from g to r: | Upper limit on d: |
Paired-samples t-test
Inputs
| Sample 1 | Sample 2 |
|---|---|
| Mean: | Mean: |
| Standard deviation: | Standard deviation: |
| Number of pairs: | r: |
| Confidence Interval: % | |
| Average | Repeated measures |
|---|---|
Results (CI using noncentral t distribution)
| Hedges's g - average (recommended): | Lower limit on d: |
| Hedges's g - repeated measures: | Upper limit on d: |
Odds/risk/absolute ratios & Number needed to treat
Inputs
| Outcome Frequency | ||
| Yes | No | |
| Treatment | ||
| Control | ||
| Method (Odds-ratio): | ||
| Method (Relative-risk): | ||
| Compute relative risk reduction in place of relative risk?: | ||
| Confidence Interval: % | ||
Results
| Odds ratio: | Risk ratio/Relative risk: |
| Lower limit on odds ratio: | Lower limit on risk ratio: |
| Upper limit on odds ratio: | Upper limit on risk ratio: |
| Number needed to treat: | Absolute risk: |
Partial eta-squared (Fixed effects)
Inputs
| F-value: | Confidence Interval: % |
| Numerator degrees of freedom: | Denominator degrees of freedom: |
It is recommended that you use the 90% CI if you have an alpha level of 5%.
Results (CI using noncentral F distribution)
| Partial eta-squared: | Lower limit on partial eta-squared: |
| Partial omega-squared: | Upper limit on partial eta-squared: |
| Cohen's f: | Lower limit on Cohen's f: |
| Upper limit on Cohen's f: | |
Partial eta-squared and omega-squared calculated here should only be interpreted if all your factors are manipulated not observed (such as gender), and you have no covariates.
Additionally, the confidence intervals produced here will differ from the confidence intervals produced in the OLS section. The calculation for the intervals returned here assumes the predictors are planned/fixed as in an experiment.
R-squared (OLS)
Inputs
| R-squared: | Confidence Interval: % |
| Numerator degrees of freedom: | Denominator degrees of freedom: |
It is recommended that you use the 90% CI if you have an alpha level of 5%.
Results
| Lower limit on R-squared: | Upper limit on R-squared: |
I have run out of resources to sustain fitting the multilevel models, so for now, the ICC and multilevel R-squared sections are down.
Intraclass Correlation Coefficient
Inputs
Export all your variables into a csv file. The first row has to be the variable names - without spaces within variable names. To minimize problems, files should be ASCII and should not contain missing values.
Method:Results - CI are always calculated from One-Way ANOVA (95% CI)
| Estimate of ICC: | |
| Variance between: | Variance within: |
| Lower limit on ICC: | Upper limit on ICC: |
| Clusters analyzed: | Average per cluster (k): |
| Design effect (DEFF): | Root DEFF (DEFT): |
Note: Average per cluster is less than mean for unbalanced designs.
I have run out of resources to sustain fitting the multilevel models, so for now, the ICC and multilevel R-squared sections are down.
HLM / multilevel Pseudo R-squared
Inputs
Export all your variables into a csv file. The first row has to be the variable names - without spaces within variable names. To minimize problems, files should be ASCII and should not contain missing values.
Optimization Method:Results
| Marginal R-squared: | Conditional R-squared: |
| Variance between: | Variance within: |
| Average random effect: | Residual ICC: |
| Clusters analyzed: | Model converged?: |
Check the results for convergence. If they do not converge, try another optimization method from the drop down menu above.
Please contact me with questions and suggestions at james.uanhoro@unt.edu.
Pull requests welcome on repo, where formulae alongside sources can be found.
If you would like to cite this website, you can use the citation below, it's APA. Thank you.
Uanhoro, J. O. (2017). Effect size calculators. Available online at: https://effect-size-calculator.herokuapp.com/.